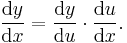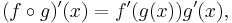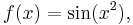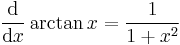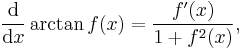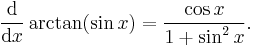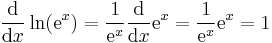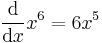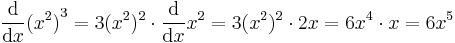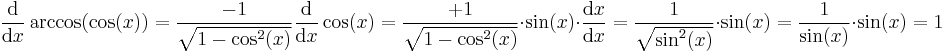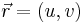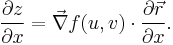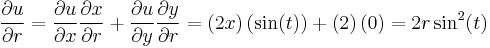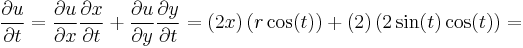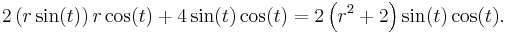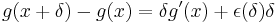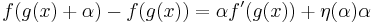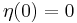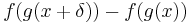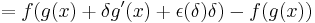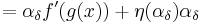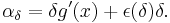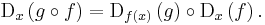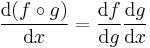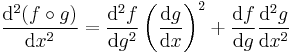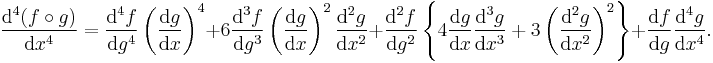Chain rule
| Topics in Calculus | ||||||||
|---|---|---|---|---|---|---|---|---|
| Fundamental theorem Limits of functions Continuity Mean value theorem
|
In calculus, the chain rule is a formula for the derivative of the composition of two functions.
In intuitive terms, if a variable, y, depends on a second variable, u, which in turn depends on a third variable, x, that is y = y(u(x)) , then the rate of change of y with respect to x can be computed as the rate of change of y with respect to u multiplied by the rate of change of u with respect to x. Schematically,
Contents |
Informal discussion
- For an explanation of notation used in this section, see Function composition.
The chain rule states that, under appropriate conditions,
which in short form is written as
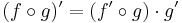 .
.
Alternatively, in the Leibniz notation, the chain rule is
The chain rule can be applied to as many composed functions as needed:
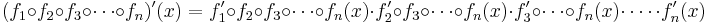 .
.
In integration, the counterpart to the chain rule is the substitution rule.
Theorem
The chain rule in one variable may be stated more completely as follows.[1] Let g be a real-valued function on [a,b] which is differentiable at c ∈ [a,b]; and suppose that f is a real-valued function defined on an interval I containing the range of g and suppose further that g(c) is an interior point of I. If f is differentiable at g(c), then
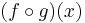 is differentiable at x = c, and
is differentiable at x = c, and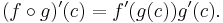
Examples
Example I
Suppose that a mountain climber ascends at a rate of 0.5 kilometers per hour. The temperature is lower at higher elevations; suppose the rate by which it decreases is 6 °C per kilometer. To calculate the decrease in air temperature per hour that the climber experiences, one multiplies 6 °C per kilometer by 0.5 kilometer per hour, to obtain 3 °C per hour. This calculation is a typical chain rule application.
Example II
Consider the function f(x) = (x2 + 1)3. It follows from the chain rule that

In order to differentiate the trigonometric function
one can write:
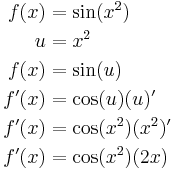
Example III
Differentiate arctan(sin x).
Thus, by the chain rule,
and in particular,
Example IV
An illuminating exercise is to compute the derivatives of functions that one already knows, but use the chain rule instead.
- Example 4.1
Rewriting x as 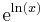 , we have
, we have
- Example 4.2
Rewriting x as 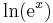 , we have
, we have
- Example 4.3
Rewriting 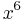 as
as 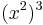 , we have
, we have
- Example 4.4
Rewriting x as  , we have
, we have
In this example, one has to be careful about the domain and range, but we can pretend we are considering only a microscopic portion of the graph.
Chain rule for several variables
The chain rule works for functions of more than one variable.[2] Consider the function z = f(x, y) where x = g(t) and y = h(t), and g(t) and h(t) are differentiable with respect to t, then
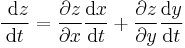 .
.
Suppose that each argument of z = f(u, v) is a two-variable function such that u = h(x, y) and v = g(x, y), and that these functions are all differentiable. Then the chain rule would look like:
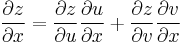 ,
,
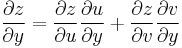 .
.
If we consider
above as a Cartesian vector function, we can use vector notation to write the above equivalently as the dot product of the gradient of f and a derivative of  :
:
More generally, for functions of vectors to vectors, the chain rule says that the Jacobian matrix of a composite function is the product of the Jacobian matrices of the two functions:
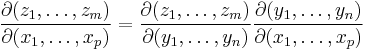 .
.
- Example
Given 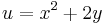 where
where 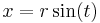 and
and 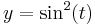 , determine the value of
, determine the value of  and
and 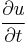 using the chain rule.
using the chain rule.
and
Proof of the chain rule
Let f and g be functions and let x be a number such that f is differentiable at g(x) and g is differentiable at x. Then by the definition of differentiability,
where ε(δ) → 0 as δ → 0. Similarly,
where η(α) → 0 as α → 0. Define also[3] that
Now
where
Observe that as δ → 0, αδ / δ → g′(x) and αδ → 0, and thus η(αδ) → 0. It follows that
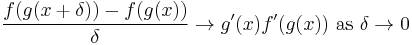 .
.
To prove the multivariate chain rule, we will deal with the case of functions of two variables; a similar proof can be constructed for functions of three or more variables. Let x(t), y(t) be differentiable functions of t and assume f(x, y) has a gradient. If we set 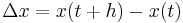 and
and 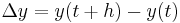 , then we have:
, then we have:
-

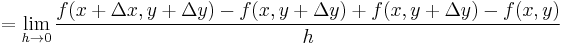
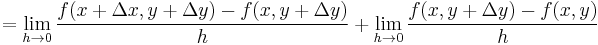 .
.
When x is constant, we can regard 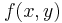 as a function
as a function 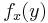 of
of 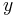 . Thus the limit on the right is equal to the derivative of
. Thus the limit on the right is equal to the derivative of 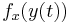 , which by the single variable chain rule is
, which by the single variable chain rule is 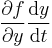 .
.
To calculate the limit on the left, regard 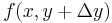 as a function
as a function 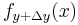 of
of 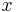 . By the mean value theorem, we can select a real number
. By the mean value theorem, we can select a real number ![\,c \in [x, x + \Delta x]](/I/9ad8498cfba30c05e3c069f31ff18c61.png) such that the numerator on the left limit is equal to
such that the numerator on the left limit is equal to 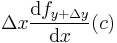 . So the left limit is equal to
. So the left limit is equal to 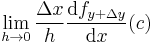 , which equals
, which equals 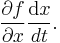
Thus, it follows that
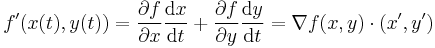 .
.
The fundamental chain rule
The chain rule is a fundamental property of all definitions of derivatives and is therefore valid in much more general contexts. For instance, if E, F and G are Banach spaces (which includes Euclidean space) and f : E → F and g : F → G are functions, and if x is an element of E such that f is differentiable at x and g is differentiable at f(x), then the derivative (the Fréchet derivative) of the composition g o f at the point x is given by
Note that the derivatives here are linear maps and not numbers. If the linear maps are represented as matrices (namely Jacobians), the composition on the right hand side turns into a matrix multiplication.
A particularly clear formulation of the chain rule can be achieved in the most general setting: let M, N and P be Ck manifolds (or even Banach-manifolds) and let
- f : M → N and g : N → P
be differentiable maps. The derivative of f, denoted by df, is then a map from the tangent bundle of M to the tangent bundle of N, and we may write
In this way, the formation of derivatives and tangent bundles is seen as a functor on the category of C∞ manifolds with C∞ maps as morphisms.
Tensors and the chain rule
See tensor field for an advanced explanation of the fundamental role the chain rule plays in the geometric nature of tensors.
Higher derivatives
Faà di Bruno's formula generalizes the chain rule to higher derivatives. The first few derivatives are
See also
- Inverse chain rule
- Triple product rule
- Leibniz integral rule
- Leibniz rule (generalized product rule)
References
- ↑ Apostol, Tom (1974). Mathematical analysis (2nd ed. ed.). Addison Wesley. Theorem 5.5.
- ↑ "The Multivariable Chain Rule". http://www.math.hmc.edu/calculus/tutorials/multichainrule/. Retrieved 2009-11-06.
- ↑ To see that this is needed, suppose for example that g is a constant function.
External links
- Weisstein, Eric W., "Chain Rule" from MathWorld.